Insertion/Deletion in 2-3 Tree

Insertion: 

            Let we create 2-3 tree by inserting elements:

                                                        20, 30, 40, 50, 60, 10, 15, 70, 80

        

    Insert 20,30:

            Now we insert these two element in a single node as it can hold 2 elements so, 

    Insert 40:

            Node is already full so split the node

            In splitting:

1. We take two nodes left and right and a root node
2. Left node contain smallest element
3. Right node contain greatest element
4. Root node contain middle element and take lest and right as child

            So the final tree will be:

    Insert 50:

            50 is greater than 40 and after 40 a blank space so insert 50 in that blank space:

    Insert 60:

            60 is greater than 50 but there is no space for 60 so split, after splitting the root element will move to the root that contain 30 b/c there is an empty space in that node, so final tree will be:

    Insert 10:

            10 is smaller than 20 and the node that contains have blank space so insert 10 in that node:

   

    Insert 15:

            15 will come that node that contain 20 b/c 10<15<20, so split the node.

            After splitting the 15 will move to node containing 30 and 50 so split this node too.

    Insert 70:

            70 is is greater than 60 so it will be inserted in node that contain 60, so final tree:

    Insert 80:

            80 is greater than 70 so it will be inserted in  node that contain 70, but there is not blank space so we have to shift, so the final tree will be:

Deletion:

    We will delete elements from above tree. There are many cases, we will discuss one by one.

    Case 1: Delete from completely filled node

            Directly delete the element and reset the node

    

    Case 2: Delete from half filled node by Delete and merge

            The node will become blank so we apply merge, reverse process of split

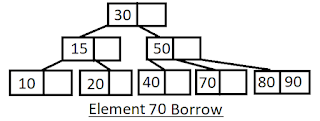
    Case 3: Delete from half filled node by Delete and borrow

            Node will borrow from parent and parent borrow from left child

    Let us understand using some examples:

        

Eg-1: Delete 90 from given tree: We will apply case 1

Eg-2 Delete 80 or 60 from above tree, apply case 2

    a. Delete element 80

        Step 1: Delete element 80 and the node will become empty

        Step 2: Merge meddle, parent and left node means revert back splitting

    b. Delete element 60

        Step 1: Delete element 60 and node will become empty

        Step 2: Merge meddle, parent and left node

        Step 2: [Alternate] Merge right, parent and meddle

Eg-3 Delete 60 from given tree, apply case 3

    

    Step 1: Delete element 60 and node will become empty

    Step 2: Borrow 70 from parent

    Step 3: Element 80 borrowed by parent

Note: Always check if borrowing is possible anyhow, don't apply merge

A Good example to check why check borrowing before merge:

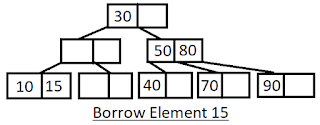
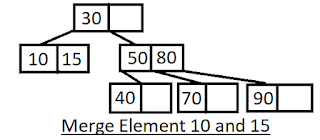
    Remove 20 from given tree:

        Step 1: Delete element 20 from given tree

        Step 2: Borrow 15 from parent [Also check for merge]

             After merge operation tree violate the property as all leaf are not at same level

    Step 3: Borrow 30 from parent

    Step 4: Borrow 50 from parent

    Step 5: Correct the Nodes

Delete Non-Leaf node:

    Eg-1 Delete 50 from from above resulted tree

        

        Step 1: We can borrow element from left sub-tree so apply operations using left

        Step 2: Delete 50 and put 40 as its predecessor at that position [as in BST]

        Step 3: Borrow 30 by its meddle and 15 by its parent

    Eg-2: Delete 40 from above resulted tree

        Step 1: We can't borrow any element so put predecessor at its position

        Step 2: Here also we can't borrow so apply merge

        Step 3: To correct the tree apply merge again