Insertion/Deletion in Red-Black Tree

 According the property of Red-Black tree, no two Red node come together (as Parent-Child relation). So if it happens then we have to reordering the tree either by recoloring or by rotation.

Note: Here NULL will considered as Black node

If the uncle of the conflicting child is red:

        Apply Recoloring:

                If G is root node then change it to black, also check if parent of G is red, if yes apply reordering recursively

If the uncle of the conflicting child is Black:

        Apply Rotation:

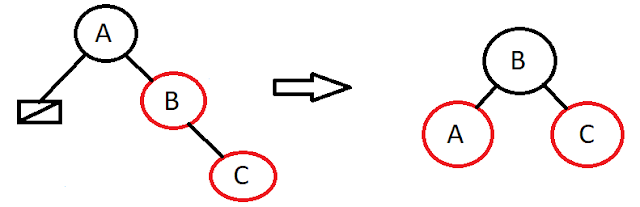
                Zig-Zig Rotation: This is similar to LL/RR rotation:

                Zig-Zag Rotation: This is similar to LR/RL rotation:

Let us create a tree by using the following nodes:

            10, 20, 30, 50, 40, 60, 70, 80, 4, 8

    Insert 10:

        As every insertion will be red so 10 will be red but it is the root node so it will become black

    Insert 20:

        20 > 10 so it will be on right side of 10 and there is no conflict b/w Red so no reordering

    Insert 30:

        30 > 20 so it will be inserted right side of 20 and red conflict occur so reordering.

        Here we do Rotation b/c uncle of 30 is black

    Insert 50:

        50 > 30 so it will be inserted right side of 30 and red conflict occur so reordering.

        Here we do Recoloring b/c uncle of 50 is red

        As the 20 is root node so it will be black so the final tree will be

Insert 40:

        40 < 50 so it will become left child of 50

        Uncle of 40 is black so apply Rotation

Insert 60:

        60 > 50 so it will become right child of 50

        Uncle of 60 is red so apply Recoloring

Insert 70:

        70 > 60 so it will become right child of 60

        Uncle of 60 is black so apply Rotation

Insert 80:

        80 > 70 so it will become right child of 70

        Uncle of 80 is red so apply Recoloring

        There is red conflict b/w 40 and 60 and uncle of 60 is black so apply Rotation

Insert 4:

        4 < 10 so it will become left child of 10

        No red conflict so proceed without reordering

Insert 8:

        8 > 4 so it will become right child of 4

        Uncle of 8 is black so apply Rotation

Final Tree